Option pricer based on Heston and FDM

Option Pricer based on Heston's stochastic vol model

Governing stochastic equation for the underlying in the risk neutral space

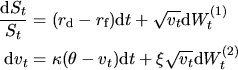
Numerical results

	price	relative error
result of the f.d.m.
analytical solution (Heston)
analytical solution (Lipton)

Dimension of the according bessel process as indicator for numerical accuracy:

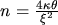= 0.86
should be greater or equal two for accurate results

option
time to maturity			strike
down and out barrier			up and out barrier
underlying characteristics
domestic rate			foreign rate
spot			initial volatility
parameters of volatility
longterm average			strength of m.r.
vol of vol			correlation
discretisation parameters of the finite difference method
grid points in spot			grid points in vol
grid points in time

Draw a sample path with these parameters

References and source code

The programme which implements the finite difference method is part of my diploma thesis. Details about the theoretical background and improvements of the numerical scheme to obtain more accurate numerical results can be found there.

The source code of the analytical solution based on the paper of Heston has been implemented by Gunter Winkler and is available here under the GNU General Public License.

The method to find an analytical solution based on Lipton is examined in the diploma thesis by Oliver Faulhaber. There you can also download the algorithms written in Mathematica and Visual Basic.

Limitations

The programme using the finite difference scheme is in a very early development stage and has to be considered as experimental. The results might be unreliable under certain parameter constellations.
Input parameters are always checked and are redefined if internally defined minimum or maximum bounds are exceeded.