Mathematical Model

Let us consider a simple model to describe the development of a population. In this model we have only one type of creature and a limited supply of food. The quantum of food available should be constant for each time period (e.g. each year) and independent of the population. The population is characterised by two parameters. The maximal growth rate is the growth rate per time period if boundless food was available. This would nearly the case if our population consists of only a few creatures because they would have almost as much as they want to eat. The other parameter is the maximum number of creatures who can live in the area. The limitation is due to limited food and the minimum requirement of food each creature needs to live. If there are more creatures than the maximum number, all would have died because none would have got enough to eat.

$n_i\in\mathbb {N}$	$\cdots$	number of creature in our population at time $i\in\mathbb {N}_0$
$\lambda_0\in\mathbb {R}^+$	$\cdots$	maximum growth rate per time period
$m\in\mathbb {N}$	$\cdots$	maximum possible number of creatures

With this information we can describe the development of the population:

$$n_{i+1}=\lambda(n_i)\cdot n_i$$

Where $\lambda:\mathbb {N}\to\mathbb {R}$ is the growth rate dependent on the actual number of creatures. In this model we assume a linear dependence. We know the growth rate in two cases:

very few number of creatures	$\lambda(0)=\lambda_0$
maximum number of creatures	$\lambda(m)=0$

The only linear function which satisfies this, is as follows and illustrated in figure 15.

$$\lambda(n)=\frac{\lambda_0}{m}(m-n)$$

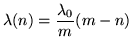
We would expect that the population would stabilise with a number of creatures $n$ so that $\lambda(n)=1$ because a growth rate of 1 means that there is no change in the number of creatures. This is satisfied if

$$n^*:=m\left(1-\frac{1}{\lambda_0}\right)$$

Figure 15: Growth rate depending on the population

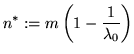
Now we can describe the development of the population:

$$n_{i+1}=\frac{\lambda_0}{m}(m-n_i)\cdot n_i$$

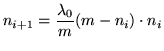
This is a quite simple equation to determine the number of creatures in a natural reservoir. We only need to know the number at the beginning $n_0$, information about the human being and the food repertoire which are represented by the constants $\lambda _0$ and $m$. Of course this is only an approximation of the reality and can only be valid if there are no other influential factors. But even this simple model shows very interesting behaviour if we change the parameters in this equation. For a better description we consider the relative population instead of the total number of creatures. The relative population is the ratio between the current population and the maximal number of creatures who can live in the natural reservoir.

$$x_i:=\frac{n_i}{m}$$

Now, we want to find an expression which shows the development of the relative population. We obtain it if we divide the last equation by $m$:

$$\frac{n_{i+1}}{m}=\lambda_0(1-\frac{n_i}{m})\cdot \frac{n_i}{m}$$

$$\Updownarrow$$

$$x_{i+1}=\lambda_0(1-x_i)\cdot x_i$$

The function $f(x):=\lambda x(1-x)$ is called the logistic function.