

Next: Examples in Nature
Up: Newton Iteration
Previous: The Method
We consider the complex function
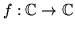 with
with
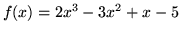 . This function can be imagined if we plot only
the absolute value
. This function can be imagined if we plot only
the absolute value 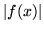 whereby we consider
whereby we consider
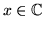 as a
two dimensional value, e.g. we plot the function
as a
two dimensional value, e.g. we plot the function
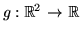 with
with
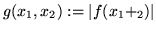 . The graph of this function
is shown in figure 10.
. The graph of this function
is shown in figure 10.
Figure 10:
Absolute value of the complex function
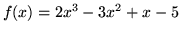
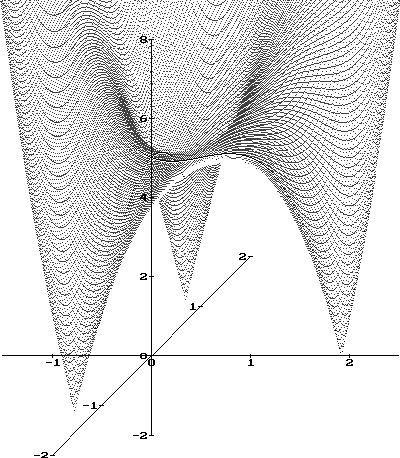 |
We can now use the Newton iteration method to obtain one of the
three roots of this function. It depends on the start value 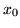 which root we will obtain. Figure 11 and 12
show which root is obtained depending on the initial value
which root we will obtain. Figure 11 and 12
show which root is obtained depending on the initial value
 .
This is done by assigning each start point
.
This is done by assigning each start point
 the colour which
hints to the root to which the newton method will converge. The result
is a fractal.
the colour which
hints to the root to which the newton method will converge. The result
is a fractal.
Figure 11:
Newton iteration with the complex function
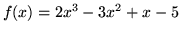
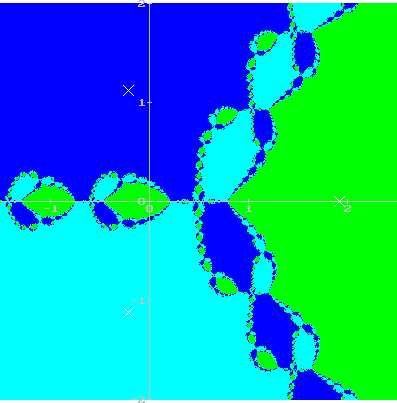 |
Figure 12:
Newton iteration (zoomed)
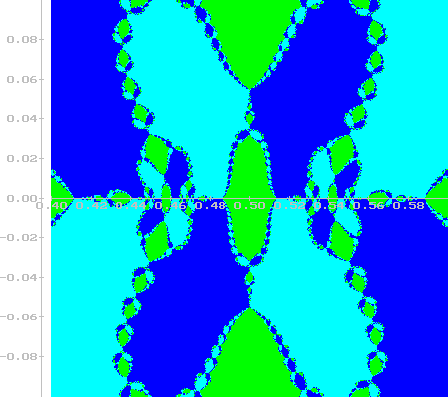 |
More colourful pictures are created if we assign each start point
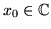 the number of iterations needed to get a sufficient numerical approximation
of the root:
the number of iterations needed to get a sufficient numerical approximation
of the root:
Figure 13:
Newton iteration, iteration depth
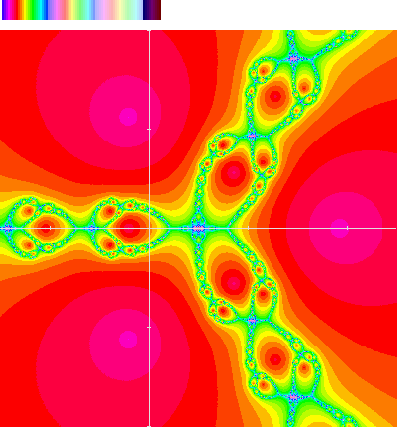 |
Figure 14:
Newton iteration, iteration depth (zoomed)
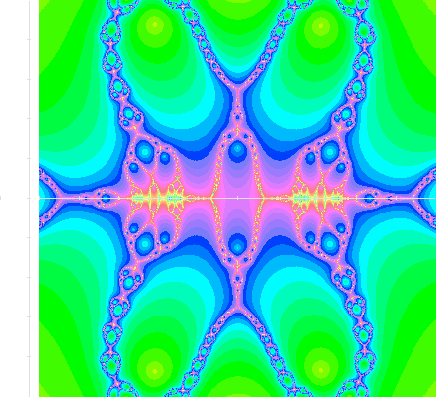 |


Next: Examples in Nature
Up: Newton Iteration
Previous: The Method
Tino Kluge
2000-12-05

![]() which root we will obtain. Figure 11 and 12
show which root is obtained depending on the initial value
which root we will obtain. Figure 11 and 12
show which root is obtained depending on the initial value
![]() .
This is done by assigning each start point
.
This is done by assigning each start point
![]() the colour which
hints to the root to which the newton method will converge. The result
is a fractal.
the colour which
hints to the root to which the newton method will converge. The result
is a fractal.
![]() the number of iterations needed to get a sufficient numerical approximation
of the root:
the number of iterations needed to get a sufficient numerical approximation
of the root: