

Next: Numerical Examples
Up: Newton Iteration
Previous: Newton Iteration
The Newton iteration method is a numerical method to approximate
a root of a function. The idea is that on a given start point
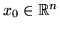 the function is approximated by a linear function and
the root of this linear function is determined. In the next
iteration this point is used in the hope that this is a better
approximation to the root of our function.
For a function
the function is approximated by a linear function and
the root of this linear function is determined. In the next
iteration this point is used in the hope that this is a better
approximation to the root of our function.
For a function
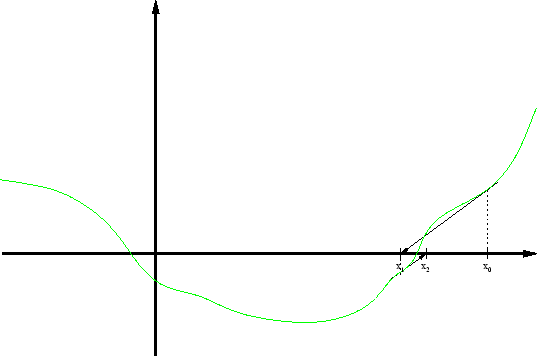
 this idea is illustrated in figure
9.
this idea is illustrated in figure
9.
Figure 9:
Idea of the Newton method
 |
The iteration method is quickly derived. The linear approximation
of a differentiable function
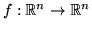 in a point
in a point
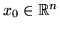 is given by
is given by
which is zero at 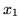 if
if
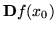 is non singular and
In a one dimensional case this iteration method simplifies to
is non singular and
In a one dimensional case this iteration method simplifies to
This idea, of course, can be applied to a complex function
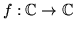 .
.
Tino Kluge
2000-12-05

![]() in a point
in a point
![]() is given by
is given by
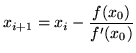
![]() .
.