Some properties of the Mandelbrot set

This section summons some properties of the Mandelbrot set first without proof, then some statements are proved.

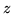
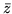
Theorem 3 (Symmetry)   The Mandelbrot set is symmetric with respect to the real axis. This means, if a complex number $z$ belongs to the mandelbrot set then this is also true for the conjigate complex number $\bar z$. (You can see this symmetry in Figure 3)

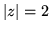
Theorem 4 (Boundary)   The Mandelbrot set is bounded. You can easily proove, thet the set must lie in the interior of the circle $\vert z \vert = 2$. (Also see Figure 3)

Theorem 5 (Itself-Similarity)   The Mandelbrot set is itself similar in a non exact sense.

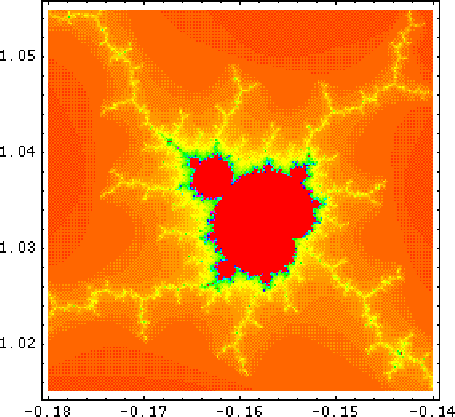
Figure 4: A plot of a zoom into the set.You can see a part of the set with the same shape as the whole set. The resolution and iteration depth is the same as in Figure 3

Theorem 6 (Real axis)   The intersection of the Mandelbrot set with the real axis is the real interval $[-2,1/4]$

Theorem 7 (connected set)   The mandelbrot set is a connected set. This result seems to contradict every picture of the set, where you think that the set consists of separated insuli.(See Figure 5)

Figure 5: A plot of a zoom into the set. You can see some connected insuli of the Mandelbrot set

Theorem 8   Fractal dimension of the border The border of the Mandelbrot set is a fractal structure with not yet known fractal dimension.