

Next: Examples of Fractals
Up: Theoretical Methods for Fractals
Previous: Bifurcations
Definition 1 (The logistic function)
The function
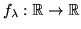
with
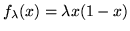
is called the logistic function.
The logistic function is often used in relation with the fix-point
iteration. For example the development of a population can be
described by
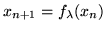 (see also section 4.1).
(see also section 4.1).
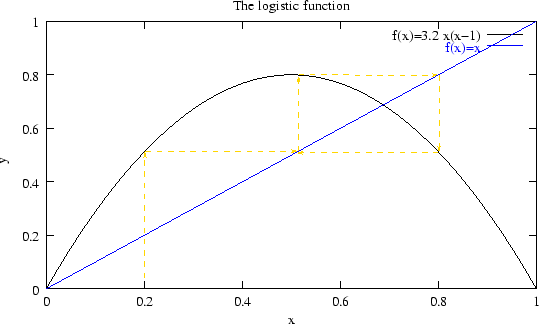
For
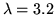 the logistic function is plotted in figure 1.
As we can see for this parameter the logistic function has an stable
two orbit attractor.
the logistic function is plotted in figure 1.
As we can see for this parameter the logistic function has an stable
two orbit attractor.
Figure 1:
The logistic function
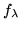 for
for
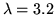
 |
Theorem 1
The Fix-point of the logistic function
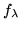
is at
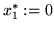
and at
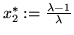
.
The second fix-point
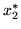
is stable for
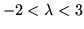
and
instable for
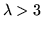
.
Proof.
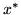
is a fix-point if and only if
We know that the fix-point is stable if
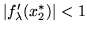
.
On the other hand the fix-point
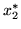
is instable if
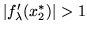
.

Theorem 2
The logistic function
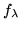
has an stable two orbit system
if
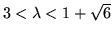
with the points
Proof.
Obviously
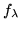
has an stable two orbit system if and only if
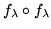
has there a stable fix-point. Therefor
we have to examine
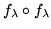
.
A fix-point of
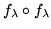
is a value
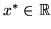
which satisfies the equation
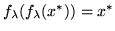
:
This is the case if and only if
The first derivative of
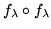
in the last two
points is exactly
of which the absolute value is smaller than one for all
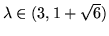

The function
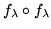 is represented for
is represented for
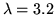 in figure 2.
in figure 2.
Figure 2:
The logistic function
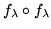 for
for
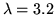
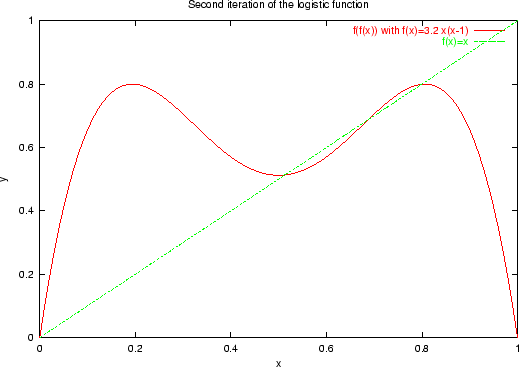 |
For higher values
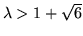 you can show that the orbit splits
into 8 points then into 16, 32, 64 etc points. The limes is reached
at about
you can show that the orbit splits
into 8 points then into 16, 32, 64 etc points. The limes is reached
at about
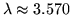 . The orbit for this limes is a
Cantor set.
. The orbit for this limes is a
Cantor set.


Next: Examples of Fractals
Up: Theoretical Methods for Fractals
Previous: Bifurcations
Tino Kluge
2000-12-05
![]() (see also section 4.1).
(see also section 4.1).
![]() the logistic function is plotted in figure 1.
As we can see for this parameter the logistic function has an stable
two orbit attractor.
the logistic function is plotted in figure 1.
As we can see for this parameter the logistic function has an stable
two orbit attractor.
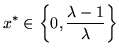
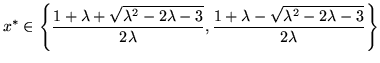
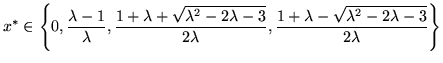
![]() is represented for
is represented for
![]() in figure 2.
in figure 2.
![]() you can show that the orbit splits
into 8 points then into 16, 32, 64 etc points. The limes is reached
at about
you can show that the orbit splits
into 8 points then into 16, 32, 64 etc points. The limes is reached
at about
![]() . The orbit for this limes is a
Cantor set.
. The orbit for this limes is a
Cantor set.