

Next: Continuous System - Pendulum
Up: Discrete System - Population
Previous: Numerical Simulation
The equation to simulate the population in the case we have considered
is quite simple because it is a quadratic function:
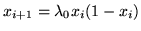 . But it shows a very rich variety of
different behaviours if we change the parameter (maximum growth rate)
. But it shows a very rich variety of
different behaviours if we change the parameter (maximum growth rate)
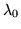 . It can be shown that for a certain value for
. It can be shown that for a certain value for 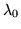 (which is approximately
(which is approximately 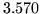 ) the attractor is a Cantor set.
That is why we obtain a fractal for some values of
) the attractor is a Cantor set.
That is why we obtain a fractal for some values of 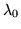 .
.
Tino Kluge
2000-12-05